Monte Carlo auf dem Schreibtisch

Dr. Konrad Reuter ist freischaffender Dozent und Berater zu Qualitätsmanagement und Statistik, Leipzig

Wikipedia schreibt :„Monte-Carlo-Simulation oder Monte-Carlo-Studie, auch: MCSimulation ist ein Verfahren aus der Stochastik, bei dem sehr häufig durchgeführte Zufallsexperimente die Basis darstellen. Man versucht dann, aufgrund der Ergebnisse mit Hilfe der Wahrscheinlichkeitstheorie analytisch unlösbare Probleme im mathematischem Kontext numerisch zu lösen. Als Rechtfertigung wird dabei vor allem das Gesetz der großen Zahl gesehen. Die Zufallsexperimente können entweder real durchgeführt werden, etwa durch Würfeln, oder durch die Erzeugung von Zufallszahlen. Heutzutage können computergenerierte Zufallsvorgänge in beinahe beliebig großem Umfang simuliert werden.“ [1]

Der Schlüssel für die Anwendung dieser Methode mit Excel liegt in der weniger bekannten Funktion ZUFALLSZAHL(). Dreistellige gleichverteilte (0;1) Zufallszahlen können schon auf statistischen Taschenrechnern erzeugt werden. Dass diese Zufallszahlen „Pseudozufallszahlen“ sind, soll zunächst nicht weiter stören. Sollten jedoch „echte“ Zufallszahlen gewünscht werden, so sind bereits sehr preiswert physikalische Zufallsgeneratoren erhältlich [7]. Für den Praktiker bietet die Zufallszahl eine exzellente Unterstützung bei der Auswahl von Teilen für eine Stichprobe. Insofern die Teile nummeriert sind, können aus dem benannten Bereich Zufallszahlen ähnlich einer Lottomaschine gezogen werden. Damit wird objektiv der Forderung entsprochen, dass Teile zufällig zu entnehmen sind.

Zufallszahlen in Excel sind 15-stellige Zahlen, gleichverteilt im Intervall (0,1). Ein wichtiger Schritt für die Anwendung auf praktische Probleme liegt in der Erzeugung von Zufallszahlen nach gewünschten Verteilungsfunktionen. Für eine Reihe von Verteilungen ist dies mit Excel ebenfalls problemlos möglich. Z.B. liefert die Funktion =NORMINV(ZUFALLSZAHL();Mittelwert;Standardabw) eine normalverteilte Zufallsvariable mit gewünschtem Mittelwert m und Standardabweichung s.

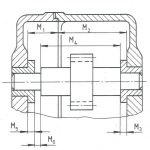
Viele Erzeugnisse des Maschinenbaues oder der Elektroindustrie sind aus Baugruppen oder Einzelteilen zusammengesetzt. Die geometrische Funktionseigenschaft wird anschaulich durch eine Verkettung der Einzelmaße in der Montage dargestellt.

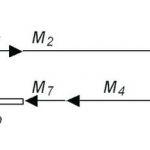
„Eine Maßkette ist die Aneinanderreihung von tolerierten Einzelmaßen Mi, die in einem technischen System zusammenwirken, und dem von ihnen abhängigen Schlussmaß M0. Die Maße M0 und Mi bilden bei ihrer schematischen Darstellung einen geschlossenen Linienzug“. [2]

Die klassische Berechung zur Maßkette geht nach der worst case Methode von den jeweiligen Kleinst- und Größtmaßen Mi aus, um das Schlussmaß M0 zu ermitteln. Dass diese Vorgehensweise der Realität einer Serienfertigung nicht recht entspricht, hat zu verschiedenen Versuchen geführt, Statistik ins Spiel zu bringen. Die früheren Methoden z.B. der zurückgezogenen DIN 7186 T1 8/74 waren aber ohne PC zu umständlich. Bekannt ist auch das RMS Verfahren.

Die Monte-Carlo-Simulation geht das Problem der Maßkette ganz anschaulich an. Für jedes Maß Mi sind Mittelwert, Streuung und Verteilungsmodell festzulegen. Ausgangspunkt dafür können aus der Praxis stammende Erfahrungen oder sinnvolle Annahmen sein. Eine solide SPC Welt im Unternehmen bzw. die realistische Ermittlung von Prozessmodellen (z.B. nach ISO 21747) erfahren hierbei eine gebührende Aufwertung. Der Dialog zwischen Fertigern und Konstrukteuren gewinnt an neuem Interesse.

Wie auch in der realen Fertigung die Teile montiert werden, so werden in einer Tabelle die simulierten Maße entsprechend der Maßkette zusammengebaut.

Ausgangspunkt der Simulation können zunächst die Toleranzmitten sein. Für die Streuungen wurden zur Demonstration unterschiedliche cp Werte angesetzt. Das Ergebnis mit den n-mal simulierten Schließmaßen steht als Tabelle für die Auswertung nach statistischen Gesichtspunkten zur Verfügung. So können z.B. Maße geschätzt werden, die mit einer bestimmten Wahrscheinlichkeit nicht über- oder unterschritten werden.

Seinen sehr praktischen Nutzen erhält dieses Vorgehen besonders dadurch, dass die Vorgaben flexibel änderbar sind und somit ganze Szenarien schnell durchgespielt werden können [4]. Die Auswirkung einzelner Veränderungen von Qualitätslage und Streuung auf das gesuchte Schließmaß sind sofort sichtbar. Die Simulation von zwei- oder dreidimensionale Maßketten sowie auch von nichtlinearen Maßketten (z.B. das bekannte Sinuslineal) ist in Excel ebenfalls umsetzbar [3]. Muss die Voraussetzung der Unabhängigkeit der Merkmale aufgegeben werden, so ist die entsprechende Korrelation in die Simulation einzubringen. Das Verfahren wird dadurch allerdings etwas komplexer.

Der „Leitfaden zur Angabe der Unsicherheit beim Messen“, bekannt unter GUM [5], stellt zur Ermittlung der Messunsicherheit Verfahren vor, die auf dem Prinzip der Fortpflanzung von Messunsicherheiten basieren. Inzwischen ist dazu die Ergänzung Supplement 1 [11] erschienen und verfügbar, die dafür das Monte Carlo Verfahren mathematisch begründet und seine Anwendung behandelt.

Die Messunsicherheit ist grundsätzlich durch Aufstellen eines mathematischen Modells des Zusammenwirkens der relevanten Unsicherheitseinflüsse zu ermitteln. Dies ist immer eine Aufgabe des Praktikers, der seinen Messprozess kennt. Nach GUM erfolgt dann die Berechnung der Sensitivitätskoeffizienten (Empfindlichkeit) durch partielle Ableitungen nach den Einflussgrößen. Spätestens an dieser Stelle wird es für Praktiker oft schwierig, der in Normen und Richtlinien vorgestellten Mathematik noch zu folgen oder gar eigene Lösungen zu finden. Da GUM auf der Linearisierung der Modellgleichung mittels Taylorreihenentwicklung beruht, werden zusätzliche Rechnungen dann erforderlich, wenn z.B. einzelne Sensitivitätskoeffizienten zu Null werden. Die Berechung der für den Überdeckungsfaktor k erforderlichen Freiheitsgrade ist ebenfalls keine leicht nachvollziehbare Aufgabe [9]. Am Ende der Berechnungen steht ein Unsicherheitsbudget, aus dem die Einflüsse der einzelnen Unsicherheiten auf das Gesamtergebnis, der erweiterten Messunsicherheit U, erkennbar sind.

Am Beispiel der Kalibrierung eines Messschiebers soll die Vorteilhaftigkeit der Simulation vorgestellt werden. Für die klassische Berechnung nach GUM stehen verschiedene Vorschläge zur Verfügung [8, 10].

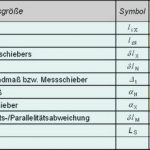
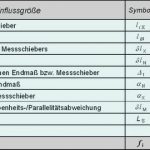
Die folgende Gleichung wird als Modell der Messunsicherheit z.B. in [9] vorgeschlagen.

Dahinter verbirgt sich aber das Problem, dass bei der Kombination von Stahl / Stahl für die Werkstoffe von Endmaß und Messschieber zwar die nominellen Ausdehnungskoeffizienten gleich sind, aber beide natürlich ebenfalls mit Unsicherheiten behaftet sind. Bei der partiellen Ableitung der Einflussgrößen würde ein Sensitivitätskoeffizient zu Null werden. Es ist also eine weitere Gleichung für diesen Punkt erforderlich (Glieder höherer Ableitung). Eine weitere Schwierigkeit ergibt sich daraus, dass beim Messschieber praktisch zwei Einflussgrößen auf die Messunsicherheit dominieren, die Auflösung der Anzeige und der Abbefehler in Verbindung mit Parallelität und Ebenheit. Dadurch wird die Berechnung des Überdeckungsfaktors k über die Freiheitsgrade nicht mehr anwendbar.

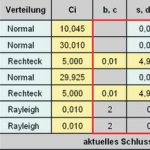
Das Monte Carlo Verfahren umgeht diese Grübeleien elegant. Die Monte-Carlo-Simulation mit Excel tabelliert alle relevanten Einflussgrößen mit ihren Verteilungen, Schätzwerten und Unsicherheitsbeiträgen z.B. nach dem Schema der Tabelle2.

An dieses Budget wird analog der Vorgehensweise bei der Tolerierung eine Spalte mit den simulierten Werten für jede Einflussgröße angekoppelt (Tabelle 3).

In der letzten Spalte sind die aktuellen Simulationswerte der Unsicherheitsbeiträge errechnet. Unter diesen Zellen (neben Modellgleichung) steckt die (relativ einfache) Modellformel, auch mit der Berücksichtigung der Unsicherheiten der Ausdehnungskoeffizienten. Ein relativ überschaubares VBA Makro spielt dann die Tabelle n-mal durch und speichert sowohl die Einflussgrößen als auch das Ergebnis jedes Simulationslaufes.

Aus einer Simulation mit n=10000 ist das Histogramm in Bild 3 entstanden.

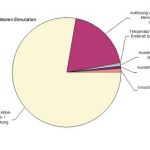
Der Vergleich der Ergebnisse zwischen klassischer Berechung (hier nicht dargestellt) und Simulation zeigt eine recht zufriedenstellende Übereinstimmung. Die Trapezform der Verteilung ist im Bild deutlich erkennbar. Der Überdeckungsgrad von 95 % muss nicht über Freiheitsgrade bzw. Sonderformeln zur Trapezverteilung [9] ermittelt werden. Bezüglich der Bestimmung des Überdeckungsgrades von 95 % schlägt das GUM Supplement 1 ein Verfahren vor, welches auf der Weite des kleinsten 95 % Bereiches beruht. Excel erlaubt auch hierbei ein einfaches Vorgehen ohne komplettes Sortieren der simulierten Werte und ohne VBA. Bei symmetrischen Verteilungen genügt die Schätzung der Quantile von 2,5 % bzw. 97,5 %. Die Bewertung der Einflussgrößen schließlich kann über eine Korrelationsrechung erfolgen [6]. Das Ergebnis zeigt Bild 4.

Die Frage nach einer sinnvollen Anzahl von Simulationsläufen, was auch immer eine Zeitfrage ist, beantwortet das Supplement mit einem adaptiven Verfahren. D.h. erste Simulationsläufe vom Umgang z.B. n= 10.000 werden nach bestimmten Kriterien ausgewertet. Werden diese Kriterien erreicht, kann die Simulation beendet werden, ansonsten erfolgt ein weiterer Simulationslauf und erneute Prüfung der Kriterien.

Mit der leichten Verfügbarkeit von respektabler Rechnerleistung und Tabellenkalkulationssoftware ist es möglich, die Vorteile von Simulationsverfahren, wie diese unter dem Begriff Monte-Carlo-Verfahren bekannt sind, auf jeden Schreibtisch zu holen. Zumindest für den Einstieg in diese Welt ist die Tabellenkalkulation nutzbar.

Einsatzgebiete der Simulation sind auch Methoden des Resampling, wie das Bootstrapping, um z.B. Vertrauensbereiche von Prozessfähigkeitskennzahlen cp zu ermitteln. Professionelle Simulationssoftware verbindet bereits Monte-Carlo-Verfahren mit FEM Berechnungen. Es darf wohl ohne Übertreibung gesagt werden, dass zukünftige Konstruktionsleistungen und Fertigungsplanungen nicht mehr ohne das Werkzeug der Monte Carlo Simulation auskommen werden. Der vorausschauende Qualitätsleiter sollte sich diesem Instrument nicht länger verschließen.

[1] http://de.wikipedia.org/wiki/Monte-Carlo-Verfahren 12.01.2007

[2] H. Trumpold, Ch. Beck, G. Richter: Toleranzsysteme und Toleranzdesign – Qualität im Austauschbau. Carl Hanser Verlag München Wien 1997

[3] K. Reuter, Moderne Methoden der statistischen Tolerierung, TQU Verlag Ulm, 2007

[4] K. Sinnreich, 3D- Toleranzmanagement, AICON 3D FORUM, Braunschweig 2008

[5] DIN V ENV 13005; Leitfaden zur Angabe der Unsicherheit beim Messen (GUM), Beuth Verlag, Berlin, 1999

[6] B.R.L. Siebert; K.-D. Sommer, Grundlagen der Monte-Carlo-Methode für die Unsicherheitsberechung, Ilmenau, 2007

[7] www.westphal-electronic.de

[8] Richtlinie DKR-R 4–3 Blatt 9.1, 1999, Kalibrierung von Messmitteln für geometrische Größen

[9] DKD-3-E2, 2002, Angabe der Messunsicherheit bei Kalibrierungen

[10] VDI/VDE/DGQv2618 Blatt 1.2, 2006, Prüfanweisung für Messschieber

[11] Supplement 1 zu GUM, „Propagation of distributions using a Monte Carlo method“, 2008

QE 508