Mit modernen elektromechanischen und servohydraulischen Prüfmaschinen lassen sich heute die vielfältigsten Beanspruchungsarten und Beanspruchungsfolgen realisieren. Die Effektivität eines Prüfsystems hängt im hohen Maße von der Fähigkeit der Prüfsoftware ab, die Reaktion des Werkstoffes auf die Beanspruchung präzise zu erfassen und mit genormten Kenngrößen zu beschreiben. Dabei ist sicherzustellen, dass die im rechnergestützten Versuch ermittelten Werkstoffkennwerte mit denen übereinstimmen, die bei konventioneller Durchführung des Versuches erhalten werden.
Bei allen Prüfaufgaben spielen wirtschaftliche Zwänge zunehmend eine bedeutende Rolle. Neben einer hohen Zuverlässigkeit und Vergleichbarkeit der Prüfergebnisse sollen die Prüfkosten möglichst klein bleiben. Diese Forderung gilt auch uneingeschränkt für das wichtigste statische Prüfverfahren – den Zugversuch. Die Anforderungen an die rechnergestützte Durchführung des Zugversuchs sind für die metallischen Werkstoffe in der neuen Fassung der DIN EN 10002-1 Anhang A festgelegt /1/.
Nach einer Beschreibung der Bestimmungskriterien für die wichtigsten Kenngrößen des rechnergestützten Zugversuches wird in diesem Beitrag gezeigt, wie die Zuverlässigkeit und Genauigkeit der Prüfung bei gleichzeitiger Senkung der Prüfzeiten durch Einsatz vom Prüfer unabhängiger Rechnerverfahren erhöht werden kann.
Werkstoffe reagieren sehr unterschiedlich
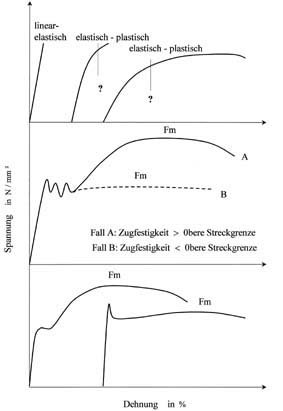
Auf eine äußere Beanspruchung reagieren die Werkstoffe sehr unterschiedlich. Die Reaktion des Werkstoffes auf eine Zugbeanspruchung wird sehr gut mit der Darstellung des Zusammenhangs von Ursache und Wirkung in Form von Kraft F-Verlängerung iL – Diagrammen oder den daraus abgeleiteten Spannung R – Dehnung «-Diagrammen veranschaulicht (Abb. 1). Derartige Diagramme geben Auskunft über das Werkstoffverhalten im elastischen Bereich (wesentlich für die Bauteilkonstruktion) und im plastischen Bereich (wichtig für die bildsame Formgebung). Sie ermöglichen ferner den schnellen Vergleich von Festigkeit und Zähigkeit zwischen den Werkstoffen oder Werkstoffzuständen.
Die in Abbildung 1 zusammengestellten Spannungs-Dehnungs-Diagramme metallischer Werkstoffe dokumentieren nicht nur das unterschiedliche Beanspruchungsverhalten der Werkstoffe sondern auch die hohen Anforderungen an die zuverlässige rechnergestützte Ermittlung der verschiedenen Kenngrößen. Insbesondere die komplexe Auswertung der unterschiedlichsten Streckgrenzenformen, die genaue und zuverlässige Ermittlung des Anstiegs der Kurven im elastischen Bereich für die Ermittlung des Elastizitätsmoduls und die quantitative Charakterisierung des elastisch-plastischen Übergangs erfordern eine Auswertesoftware, die dem tatsächlichen Werkstoffverhalten Rechnung trägt /2-6/.
Kennwertermittlung nach Norm
Für die Bestimmung der mechanischen Eigenschaften von metallischen Werkstoffen nach DIN EN 10002-1 Anhang A muss die Software der Prüfmaschine die folgenden Bedingungen erfüllen:
l Obere Streckgrenze ReH: Als obere Streckgrenze ReH ist die Spannung definiert, die dem höchsten Kraftwert vor einer Kraftabnahme von mindestens 0,5 % entspricht, wobei im nachfolgenden Dehnungsbereich von mindestens 0,05 % die vorherige Maximalkraft nicht überschritten werden darf (Abb. 2: Teilbild a).
l Untere Streckgrenze ReL: Die untere Streckgrenze ReL ist die niedrigste Spannung innerhalb von 0,2 % Dehnung nach Überschreiten der oberen Streckgrenze ReH, wenn keine Änderung der Prüfgeschwindigkeit der Maschine vorgenommen wurde (Abb. 2: Teilbild b). Für den Fall, dass keine obere Streckgrenze erkannt wird und der Kraftabfall kleiner als 0,5 % über einen Dehnbereich größer als 0,2 % ist, entspricht die maximale Kraft beziehungsweise Spannung in diesem Bereich ebenfalls der unteren Streckgrenze. Bei Änderung der Prüfgeschwindigkeit nach Überschreiten der oberen Streckgrenze können „Einschwingvorgänge“ das Werkstoffverhalten überlagern. Als untere Streckgrenze wird dann die niedrigste Spannung im Fließbereich bei Ausschluss der Einschwingerscheinungen bestimmt.
l Dehngrenzen: Für Werkstoffe ohne ausgeprägte Streckgrenze wird der Übergang elastischer – plastischer Bereich mit Hilfe von technischen Elastizitätsgrenzen zum Beispiel Rp 0,01 % oder Ersatzstreckgrenzen zum Beispiel Rp 0,2 % festgelegt. Dabei ist zu beachten, dass diese Werte durch Interpolation zwischen zwei Messwertpaaren der geglätteten Kurve bestimmt werden. Zu unterscheiden ist immer zwischen den Dehngrenzen bei nichtproportionaler und bei gesamter (totaler) Dehnung (Abb. 2: Teilbild c).
l Zugfestigkeit Rm: Die Zugfestigkeit Rm ist die Spannung, die der Höchstzugkraft Fm entspricht. Dabei ist zu beachten, dass als Höchstzugkraft die größte Kraft nach Überschreiten der Streckgrenze definiert ist (s. Bild 1: Spannungs-Dehnungs-Diagramme mit ausgeprägter Streckgrenze).
l Streckgrenzendehnung Ae: Die Streckgrenzendehnung Ae ist der Betrag der Dehnung zwischen der oberen Streckgrenze und dem Punkt der Kurve, von dem ab der Anstieg der Kurve in einem vorgegebenen Dehnungsintervall zum Beispiel 0,5 % stetig steigend ist (Abb. 2: Teilbild d). Ab diesem Punkt kann die Prüfung zur Reduzierung der Prüfzeiten mit der höchsten vorgeschriebenen Prüfgeschwindigkeit fortgesetzt werden, da der Einfluss der Prüfgeschwindigkeit auf die weiteren Kennwerte nur gering ist.
l Dehnung bei Höchstkraft Age und Agt: Die Dehnung bei Höchstkraft ist der Wert, der dem Maximum der geglätteten Spannungs-Dehnungs-Kurve entspricht. Da das Maximum sehr unterschiedlich ausgebildet sein kann, ist der ermittelte Kennwert unter anderem durch die Angabe der Bestimmungsmethode genau zu kennzeichnen. Für die Ermittlung des Maximums wird in der Norm eine Regression auf der Grundlage einer Gleichung 3. Grades empfohlen. Zu unterscheiden ist immer zwischen der nichtproportionalen (Gleichmaß) – Dehnung Age und der totalen Dehnung Agt. Die Bestimmungsgenauigkeit der Gleichmaßdehnung hängt dabei in erster Linie von der Präzision der Bestimmung des Kurvenanstiegs im elastischen Bereich und der „richtigen“ Bestimmung der Höchstzugkraft ab.
l Dehnung bei Bruch A und At: Die Ermittlung der Bruchdehnung A kann mittels einer direkten Dehnungsmessung mit einem Längenänderungsaufnehmer an der Probe oder aber auch über die Messung des Traversenweges (Wegänderungen zwischen den Probenhaltern) erfolgen. Unabhängig von der Art der Wegmessung ist aber für die Ermittlung von Bruchdehnungswerten mit rechnergestützten Prüfmaschinen auf die Definition des Bruchpunktes zu achten.
Als Probenbruch soll der Punkt genommen werden, nachdem der Kraftabfall zwischen zwei aufeinanderfolgenden Messpunkten mindestens fünfmal größer ist als bei den vorherigen Messpunkten, gefolgt von einem Abfall auf kleiner als 3 % der maximalen Zugkraft.
Die normgerechte rechnergestützte Auswertung der Spannungs-Dehnungs-Kurven stellt auch bestimmte Anforderungen an die Messwerterfassung der Prüfmaschine. So muss die Messwerterfassungsfrequenz f größer als der Mindestwert fmin sein, der aus dem Wert der oberen Streckgrenze ReH, der aktuellen Spannungszunahmegeschwindigkeit d und der Klasse q der benutzten Prüfmaschine berechnet werden kann.
d
fmin = ReH x q
Kennwerte schnell und bedienerunabhängig ermitteln
Die zuverlässige und genaue Bestimmung des Elastizitätsmoduls E (wichtig für die Berechnung der Steifigkeit von Konstruktionen und die Bewertung des Rückfederungsverhalten) sowie von Dehnungen und Dehngrenzen hängt in erster Linie davon ab, wie und mit welcher Genauigkeit sich die Lage und die Steigung der Hookeschen Gerade als Hilfsgröße für die weitere Auswertung ermitteln lässt.
In der Regel erfolgt die Prüfung mit dem vom Prüfer vorgegebenen Elastizitätsmodul Ev und die Steigung der Kurve Ep wird zunächst zwischen zwei ebenfalls vom Bediener gewählten Bezugswerten bestimmt. Nach dem Versuch kann dann überprüft werden, ob man mit den gewählten Bezugswerten tatsächlich im steilsten Bereich der Spannungs-Dehnungs-Kurve liegt. Die Art der Probeneinspannung, aber auch die Probenbeschaffenheit (zum Beispiel gebogene Drähte oder gewölbte Bleche) können den Kurvenverlauf stark beeinflussen. Für die Prüfung können deshalb keine konstanten Bezugswerte sondern nur Richtwerte verwendet werden. Die Auswirkungen der zu beachtenden Einflussgrößen auf die Genauigkeit der Bestimmung der Dehngrenze Rp 0,2 % veranschaulicht Abbildung 3. Insbesondere wird man für stark verfestigende Werkstoffe in Abhängigkeit von der Art der Bestimmung deutlich voneinander abweichende Kennwerte erhalten.
Die nachträgliche Festlegung beziehungsweise Änderung der Bezugswerte zur genaueren Ermittlung der Steigung ist nicht nur sehr zeitaufwendig sondern auch von der Erfahrung und der Arbeitsweise des Prüfers abhängig. Insbesondere bei Spannungs-Dehnungs-Kurven mit gekrümmter Hookescher Geraden hängt die Kennwertermittlung sehr vom Prüfer ab /2, 5/. Diese Faktoren beeinträchtigen sehr die Vergleichbarkeit der Prüfergebnisse zwischen verschiedenen Prüflabors und können auch zu Fehlbeurteilungen in der Qualitätskontrolle führen.
Zur Erhöhung der Zuverlässigkeit der rechnergestützten Versuchsauswertung werden deshalb in der DIN EN 10002-1 Anhang A für die Bestimmung des Kurvenanstiegs im elastischen Bereich Verfahren empfohlen, die auf der schrittweisen Auswertung von Kurvensegmenten arbeiten.
Für die Analyse der Spannungs-Dehnungs-Kurve mit mathematischen Funktionen gibt es verschiedene Vorschläge.
Wie mit zahlreichen Untersuchungen an Stählen und Nichteisenmetallen /2, 5/ nachgewiesen werden konnte, eignen sich für die Beschreibung des Anfangsbereiches der Spannungs-Dehnungs-Kurve die beiden kubischen Polynome mit Sigma s für die Spannung und Epsilon « für die Dehnung:
s = a0 + a1 · « + a2 · «2 + a3 · «3 /1/
« = b0 + b1· s + b2 · s2 + b3 · s3 /2/
a , b i = 0, 1, 2, 3 bezeichnen die Koeffizienten der kubischen Polynome.
Beim Einsatz von Rechnerverfahren ist zunächst zu sichern, dass die Analyse der Kurve innerhalb eines repräsentativen Bereichs erfolgt. Für metallische Werkstoffe mit ausgeprägter Streckgrenze ist dies der Bereich zwischen der Vorkraft und der oberen Streckgrenze, für Werkstoffe ohne ausgeprägte Streckgrenze und mit wenig ausgeprägter Hookescher Gerade ist der Bereich zwischen der Vorkraft und maximalen Kraft zu betrachten (Abb. 4). Die Vorkraft wird verwendet, um relativ einheitliche Versuchsbedingungen (Probenausrichtung, Anordnung der Probenhalter) zu erreichen. Sie darf 5 Prozent der erwarteten maximalen Zugkraft nicht überschreiten. Ferner ist eine Korrektur der Verlängerung in Abhängigkeit von der Vorkraft vorzunehmen (Abb. 3).
Für die weitergehende Analyse des repräsentativen Bereiches wurden verschiedene Wege beschritten /5/.
In Anlehnung an /2/ erwies sich auch folgende Vorgehensweise als sehr praktikabel /7/:
1. Der auszuwertende Bereich wird in n-Segmente unterteilt und das Segment mit dem größten Anstieg ermittelt. Die Anzahl n der Segmente ist in Abhängigkeit von der Geschwindigkeit des gewählten mathematischen Verfahren beziehungsweise nach der zur Verfügung stehendenden Auswertezeit festzulegen. Sie sollte nicht unter zehn liegen, anzustreben sind bis zu 50 Segmente oder auch mehr.
2. Polynom-Approximation des Kurven-Segments mit der größten Steigung: Erfahrungsgemäß wird nach zwei bis drei Durchläufen eine gute Approximation erreicht. Die so ermittelte Steigung und Lage der Kurve bilden die Grundlage für die weitere Auswertung zum Beispiel für die Ermittlungen von Dehngrenzen und Dehnungswerten für ausgewählte Punkte im Spannungs-Dehnungs-Diagramm oder für die Bestimmung des Elastizitätsmoduls.
Bei Einsatz von schnellen Berechnungsmethoden dauert die beschriebene Prozedur nur wenige Sekunden. Gegenüber der herkömmlichen Methode entsteht beim Einsatz von Rechnerverfahren ein erheblicher Zeitgewinn und subjektive Einflüsse auf die Kennwertermittlung durch den Bediener werden reduziert. Bei Ausschaltung beziehungsweise Berücksichtigung versuchsbedingter Unstetigkeiten im Anfangsbereich der Spannungs-Dehnungs-Kurven liegt die Streuung der an verschiedenen Werkstoffen ermittelten E-Moduli in einem Bereich, der zum Beispiel die Ermittlung der 0,2 %-Dehngrenze mit einer maximalen Abweichung von ± 1% erlaubt /2, 7/.
Prüfergebnisse werden vergleichbarer
Wie die vorliegenden Untersuchungsergebnisse /2, 5-7/ zeigen, bieten Rechnerverfahren eine effiziente Möglichkeit zur Bestimmung des linearen Teils der Spannungs-Dehnungs-Kurve im elastischen Bereich und damit zur Bestimmung des Elastizitätsmoduls im Zugversuch.
Sowohl für metallische Werkstoffe (Stähle, NE-Metalle) als auch für Kunststoffe werden signifikante Kennwerte ermittelt, die auch innerhalb einer Werkstoffgruppe eine eindeutige Klassifizierung gestatten. Der daraus resultierende Vorteil für die weitergehende Auswertung von Zugversuchen liegt auf der Hand. Bei allseitiger Anwendung dieser Auswertemethoden wird die Prüfung nicht nur einfacher und schneller. Auch die subjektiven Einflüsse durch den Prüfer werden unter anderem durch den Wegfall der Eingabe von Bezugswerten reduziert und die Prüfergebnisse werden werkstoffübergreifend vergleichbarer.
Mit dem Einsatz von Rechnerverfahren kann bei gekrümmten Spannungs-Dehnungs-Kurven auf das aufwendige und für genaue Messungen abzulehnende Hysterese-Verfahren verzichtet werden. Dieses Verfahren setzt voraus, dass der Nullpunkt des Spannungs-Dehnungs-Diagramms immer im Koordinatenursprung liegt. Dies ist in der Regel nicht der Fall, so dass für eine genaue Bestimmung von Dehngrenzen immer in Abhängigkeit von der ermittelten Kurvensteigung der „wahre“ Nullpunkt zu bestimmen ist (Abb. 3).
Literatur:
/1/ DIN EN 10002-1, Anhang A, Prüfung metallischer Werkstoffe, Rechnergestützter Zugversuch, 1998, Beuth-Verlag Berlin.
/2/ Hesse, B; Sonne, H.-M.; Robiller, G., Verfahren zur Steigungsbestimmung der Hookeschen Gerade im rechnergestützten Zugversuch, Thyssen Technische Berichte 2, (1990), 1, S.115 -121.
/3/ Sonne, H.-M. und Wehrstedt, A., Rechnergestützter Zugversuch, Materialprüfung 37, (1995), Heft 4, S. 102-105.
/4/ Michalzik, G. und Oliver, K., Prozessbegleitende Qualitätssicherung, Qualität und Zuverlässigkeit 41, (1996), Heft 1, S. 66-68.
/5/ Sonne, H.-M., Bestimmung des E-Moduls im Zugversuch, Vortrags- und Diskussionstagung Werkstoffprüfung 1999, 2. und 3. Dezember 1999, Bad Nauheim, S. 219 – 230.
/6/ Ledworuski, S.; Ell, M. und Kühn, H.-J., Zur Problematik der sicheren Bestimmung des E-Moduls in der mechanischen Werkstoffprüfung, Vortrags- und Diskussionstagung Werkstoffprüfung 1999, 2. und 3. Dezember 1999, Bad Nauheim, S. 231- 240.
/7/ Michalzik, G.; Oliver, K.; Wiese, L.
Anwendungsbezogene rechnergestützte Ermittlung von mechanischen Kennwerten
INNOMATA 1996 und GfKORR-Fachtagung 7.-9. Mai 1996 Dresden
/8/ Oliver, K. und Michalzik, G., Ein vollautomatisches Materialprüfzentrum, Materialprüfung 37, (1995), Heft 9, S. 332 – 336.
Weitere Informationen A QE 500
Dr.-Ing. habil. Günter Michalzik, Ulm